Parametric elipses.
Joshua DuMont
Derive
the parametric equations for the locus of a point (x, y) on a line segment that
is moved so that one end is on the x-axis and the other end is on the y-axis.
A
way to parameterize this curve is by the angle t that the line segment makes
with the x-axis. In the gray triangle sin(t)=
or y=bsin(t). In the blue triangle, cos(t)=
or x=acos(t).
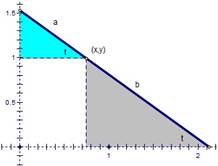
A
parameterization of the locus of the point then is:
x=acos(t),
y=bsin(t)
This
forms an ellipse, as t changes.
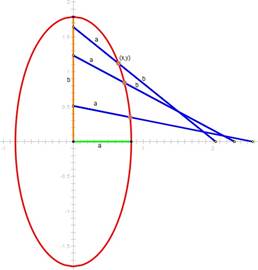
To
see this, take =cos(t)
, 
=sin(t) and square both
sides of each equation.
=
(t) ,
=
(t) Adding the left sides together and the right
sides together yields:
+
=(t)+(t) or just: +=1
Which
is the familiar form for an ellipse.
In
that form it may be that we recognize that the a value
gives the horizontal distance from the center to the ellipse, and the b value
gives the vertical distance from the center to the ellipse. This could be seen
in the parametric form just as easily. The maximum y value happens when t=
. Plugging this in we find
the point (0,b). Similarly, the maximum x value
happens when t=0. Plugging this in we get the point (a,0).
So,
for different choices of lengths for a and b we get
different ellipses.
We
needn’t have written the function in terms of the angle the segment makes with
the x-axis. If we choose to parameterize by the angle the segment makes with
the y-axis we get: x=asin(t), y=bcos(t). This turns out to
trace the same graph. Using the same method as above, we can write this in
Cartesian form as: +=1. The two
parameterizations give the same graph, but don’t follow the same path. The
first gives the point (a,0) when t=0, and moves
counterclockwise returning to the beginning point every time t is a multiple of 2π. The second gives the point (0,b) when t=0 and moves clockwise with the same period. A
different choice for parameter will affect the direction travelled, the point
at which we start and the period. Replacing t with 2t
in either of our parameterizations, for instance, doesn’t affect the process we
used above to change to Cartesian form (the graph is the same). However, it
does cause any point which previously happened at t=c to occur at t=
. In the time it took
previously to travel around the ellipse once we now travel around it twice.